如何解释 Z 分数
已发表: 2023-01-17
z 分数是一种数值测量,描述了特定值与数据集平均值的标准差数。 它用于确定特定值在数据集中的罕见或常见程度。 但是如何找到 z 分数呢? 继续阅读文章以找出答案。 z 得分可以是正数或负数,其中正 z 得分表示该值高于平均值,负 z 得分表示该值低于平均值。 我们将在本文中进一步讨论如何解释 z 得分。

内容
- 如何解释 Z 分数
- 什么是 Z 分数?
- 1. Z 分数以标准差单位衡量
- 2. Z 分数可以是正数也可以是负数
- 3. Z-scores 使您的数据与其他指标的比较变得简单
- 如何找到 Z 分数
- Z 分数与标准差
- 如何解读 Z 分数表
- 负 Z 分数意味着什么?
如何解释 Z 分数
在本文中,您将详细了解解释 Z 分数的步骤。
什么是 Z 分数?
z 分数是一种度量标准,用于量化给定值偏离数据集平均值的标准偏差数。 它用于确定数据集中特定值的稀有度或流行度。 继续阅读以了解如何解释 z 分数
让我们看看了解如何解释 z 分数的可能方法:
1. Z 分数以标准差单位衡量
在解释 z 分数时,请务必记住 z 分数是以标准差单位衡量的。 这意味着 z 分数的值告诉您特定值与数据集均值的标准差有多少。
例如,假设您有一个平均值为 50 且标准差为 10 的数据集。如果您计算特定值(例如 30)的 z 分数,并发现它是 -2,您可以将其解释为30 的值比 50 的平均值低两个标准差。
您还可以使用 z 表来确定数据集中高于或低于特定 z 分数的值的百分比。 例如,如果您的 z 得分为 1.96,您可以在 z 表中查找该值,发现数据集中大约 97.5% 的值低于该值。
2. Z 分数可以是正数也可以是负数
在解释 z 分数时,z 分数可以是正数或负数这一事实很重要,因为它可以让您确定特定值是高于还是低于数据集的平均值,以及该值在数据集中的罕见或常见程度。 在本文的后面将看到负 z 分数意味着什么
3. Z-scores 使您的数据与其他指标的比较变得简单
z-scores 允许您轻松地将数据与其他指标进行比较,这在解释 z-score 时很重要,因为它允许您将数据置于上下文中并根据您的分析做出更明智的决策。
另请阅读:从 Excel 文件中删除密码
如何找到 Z 分数
要找到给定值的 z 分数,您需要知道该值所来自的总体或样本的均值和标准差。 z-score计算公式如下:
z = (x – 均值) / 标准差
其中 x 是值,均值是总体或样本的平均值,标准差是总体或样本的标准差。
例如,假设您有 1000 人的样本,并且您想要找到一个 6 英尺高的人的 z 分数。 样本的平均高度为 5 英尺 10 英寸,标准偏差为 2 英寸。 要计算 6 英尺高的人的 z 分数,您可以使用以下公式:
z = (72 – 70) / 2 = 1
这意味着身高 6 英尺的人比平均值高出一个标准差。
如果您想找到低于均值的值的 z 分数,则 z 分数将为负数。 例如,如果值为 5 英尺 8 英寸,则 z 分数将为:
z = (68 – 70) / 2 = -1
这意味着身高 5 英尺 8 英寸的人比平均值低一个标准差。
Z 分数与标准差
下面列出了 z 分数与标准差之间的一些差异。

| Z分数 | 标准偏差 |
| 数据点与平均值的标准差数 | 衡量一组数据点围绕均值的分布或离差的量度 |
| z分数的公式是 (x – 均值) / 标准差 | 标准偏差的公式是 √((Σ(x – 平均值)^2) / n) |
| 告诉您数据点与平均值的标准差有多少 | 告诉您数据与均值的分布情况 |
| z 分数为 1.5 表示数据点比平均值高 1.5 个标准差 | 标准偏差为 10 表示数据点通常与平均值相差 10 个单位 |
因此,z-score 与标准差之间的主要区别在于,z-score 是衡量一个值与均值相差多少标准差的具体度量,而数据分布是通过标准差来量化的。
另请阅读:在工作表之间快速切换
如何解读 Z 分数表
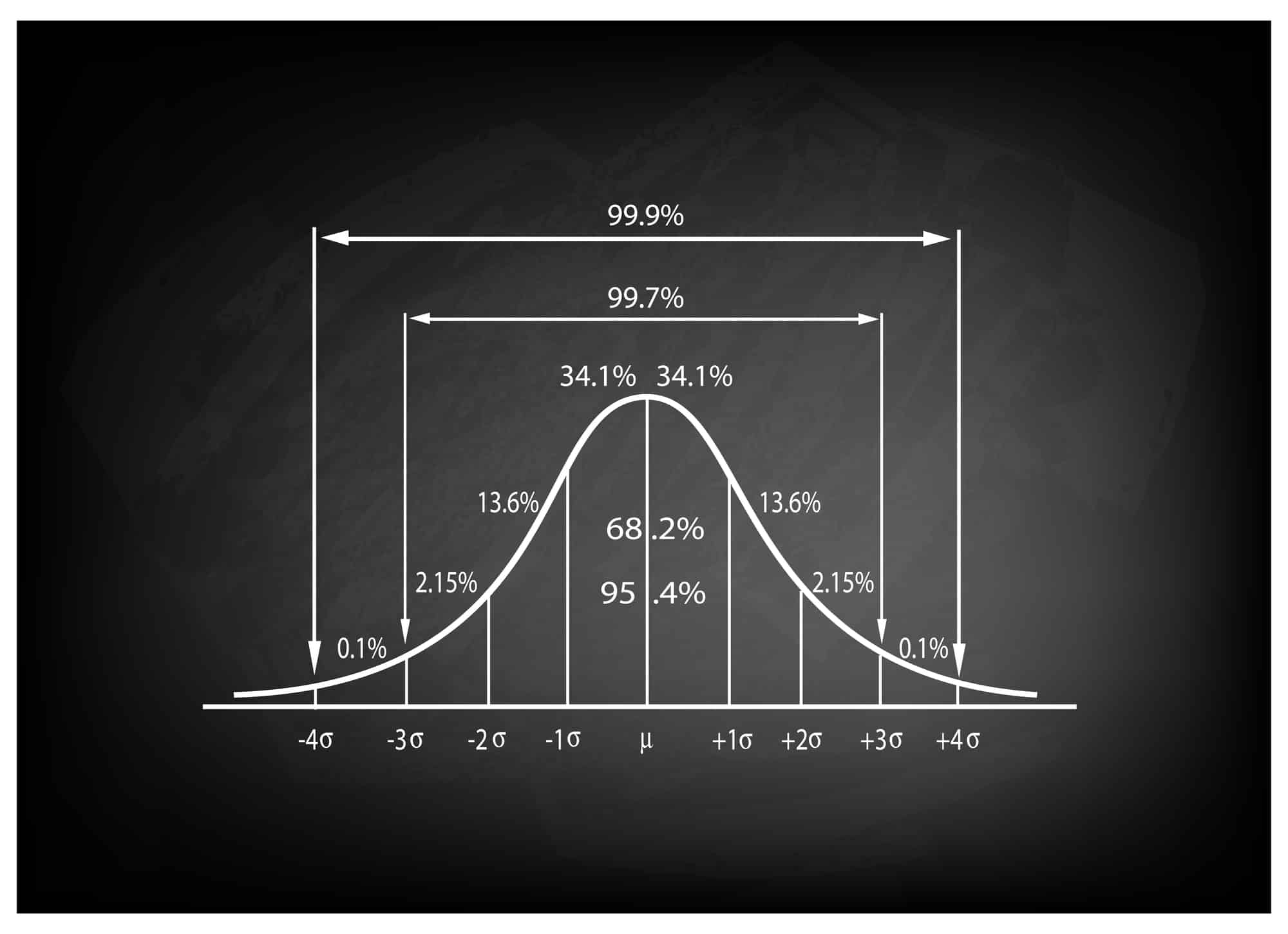
为了学习如何解释 z-score 表,首先您需要知道要查找的值的 z-score。 z 分数表通常会显示给定 z 分数范围的标准正态曲线下的面积。
例如,假设您要查找 z 得分为 1.5 的曲线下面积。 您将在 z 分数表中查找与 z 分数 1.5 对应的行,然后找到与曲线下面积对应的列。 该单元格中的值是 z 得分为 1.5 时曲线下的面积。
曲线下的面积是给定值出现的概率。 例如,如果 z 得分为 1.5 的曲线下面积为 0.9332,则 z 得分为 1.5 的值出现的概率为 93.32%。
请务必注意,z 分数表通常基于标准正态曲线,这是一个均值为 0 且标准差为 1 的正态分布。如果您的 z 分数基于不同的均值和标准差,在表中查找之前,您需要使用 z 分数转换公式将其转换为标准正态分布。
另请阅读:如何在 Clubhouse Android 上更改用户名和名称
负 Z 分数意味着什么?
负 z 分数表示该值小于平均值。 换句话说,它低于平均值。
为了更好地理解,让我们以前面的示例为例,假设您有 1000 人的样本,并且您想要找到一个身高 5 英尺 8 英寸的人的 z 分数。 样本的平均高度为 5 英尺 10 英寸,标准差为 2 英寸。 要计算 5 英尺 8 英寸高的人的 z 分数,您可以使用以下公式:
z = (68 – 70) / 2 = -1
这意味着身高 5 英尺 8 英寸的人比平均值低一个标准差。
一般来说,z-score 为 0 表示值恰好位于平均值,z-score 为 1 表示值比平均值高一个标准差,z-score 为 -1 表示值是低于平均值一个标准差。
常见问题 (FAQ)
Q1。 Z-Score 如何在现实生活中使用?
答。 Z 分数,也称为标准分数,是一种度量标准,用于确定一个数字与数据集的平均值之间有多少标准偏差。 查找数据中的离群值、异常值和奇怪模式是统计学、数据分析和机器学习中的典型任务。
Q2。 什么会产生负 z 分数?
答。 负 Z 分数表示值低于数据集的平均值。 通常,任何小于数据集平均值的值都会产生负 Z 分数。
Q3. Z表告诉你什么?
答。 Z 表,也称为标准正态表,是一种统计表,显示给定值在标准正态分布内出现的概率。
推荐的:
- 如何观看已删除的 YouTube 视频
- Modbus 从站原理完整指南
- 如何在 Google 表格中索引匹配多个条件
- GNSS 是如何工作的?
要解释 Z 分数,重要的是要考虑数据集的均值和标准差,以及使用 Z 分数的环境。 我们真诚地希望我们能提供一些关于如何解释 z 分数的信息。 请在下面的评论部分告诉我们您的疑问和建议。
