Como interpretar o Z Score

Um escore z é uma medida numérica que descreve o número de desvios padrão de um valor específico da média de um conjunto de dados. Ele é usado para determinar o quão raro ou comum um determinado valor é em um conjunto de dados. Mas como encontrar o escore z? Continue lendo o artigo para descobrir. Um escore z pode ser positivo ou negativo, onde um escore z positivo indica que o valor está acima da média e um escore z negativo indica que o valor está abaixo da média. Discutiremos como interpretar o escore z mais adiante no artigo.

Como interpretar o Z Score

Neste artigo, você conhecerá detalhadamente os passos para interpretar o escore Z.

O que é o Z Score?

Uma pontuação z é uma métrica que quantifica quantos desvios padrão um determinado valor se desvia da média do conjunto de dados. É empregado para estabelecer a raridade ou prevalência de um valor específico dentro de um conjunto de dados. Continue lendo para descobrir como interpretar o escore z

Vejamos as formas possíveis de aprender a interpretar o escore z:

1. Os escores Z são medidos em unidades de desvio padrão

Ao interpretar um escore z, é importante ter em mente que os escores z são medidos em unidades de desvio padrão. Isso significa que o valor do escore z informa quantos desvios padrão um valor específico está da média do conjunto de dados.

Por exemplo, suponha que você tenha um conjunto de dados com uma média de 50 e um desvio padrão de 10. Se você calcular o escore z para um valor específico, digamos 30, e descobrir que é -2, você pode interpretar isso como significando que o valor de 30 está dois desvios padrão abaixo da média de 50.

Você também pode usar uma tabela z para determinar a porcentagem de valores no conjunto de dados que estão acima ou abaixo de uma pontuação z específica. Por exemplo, se você tiver um escore z de 1,96, poderá procurar esse valor em uma tabela z para descobrir que aproximadamente 97,5% dos valores no conjunto de dados estão abaixo desse valor.

2. Os escores Z podem ser positivos ou negativos

O fato de os escores z poderem ser positivos ou negativos é importante ao interpretar um escore z porque permite determinar se um determinado valor está acima ou abaixo da média do conjunto de dados e quão raro ou comum esse valor é no conjunto de dados. Mais adiante no artigo, veremos o que significa um escore z negativo

3. Z-scores simplificam a comparação de seus dados com outras métricas

O z-score permite que você compare seus dados facilmente com outras métricas, o que é importante ao interpretar um z-score porque permite que você coloque seus dados em contexto e tome decisões mais informadas com base em sua análise.

Leia também: Remova a senha do arquivo do Excel

Como Encontrar o Z Score

Para encontrar o escore z para um determinado valor, você precisará saber a média e o desvio padrão da população ou amostra da qual o valor veio. A fórmula de cálculo do z-score é a seguinte:

z = (x – média) / desvio padrão

Onde x é o valor, média é a média da população ou amostra e desvio padrão é o desvio padrão da população ou amostra.

Por exemplo, digamos que você tenha uma amostra de 1.000 pessoas e deseja encontrar o escore z para uma pessoa com 1,80 m de altura. A altura média da amostra é de 5 pés e 10 polegadas e o desvio padrão é de 2 polegadas. Para calcular o escore z de uma pessoa de 1,80 m de altura, você usaria a seguinte fórmula:

z = (72 – 70) / 2 = 1

Isso significaria que a pessoa com 1,80 metro de altura está um desvio padrão acima da média.

Se você quiser encontrar o escore z para um valor abaixo da média, o escore z será negativo. Por exemplo, se o valor for 5 pés e 8 polegadas, o z-score seria:

z = (68 – 70) / 2 = -1

Isso significaria que a pessoa com 5 pés e 8 polegadas está um desvio padrão abaixo da média.

Pontuação Z vs Desvio Padrão

Abaixo estão listadas algumas das diferenças entre o escore z e o desvio padrão.

pontuação Z	Desvio padrão
O número de desvios padrão de um ponto de dados é da média	Uma medida da propagação ou dispersão de um conjunto de pontos de dados em torno da média
A fórmula para o escore z é (x – média) / desvio padrão	A fórmula do desvio padrão é √((Σ(x – média)^2) / n)
Informa quantos desvios padrão um ponto de dados está da média	Diz a você como os dados estão espalhados em relação à média
Um escore z de 1,5 significa que o ponto de dados está 1,5 desvios padrão acima da média	Um desvio padrão de 10 significa que os pontos de dados estão normalmente a 10 unidades de distância da média

Portanto, a principal diferença entre o escore z e o desvio padrão é que um escore z é uma medida específica de quantos desvios padrão um valor está da média, enquanto a dispersão de dados é quantificada pelo desvio padrão.

Leia também: Alternar rapidamente entre planilhas

Como interpretar a tabela de pontuação Z

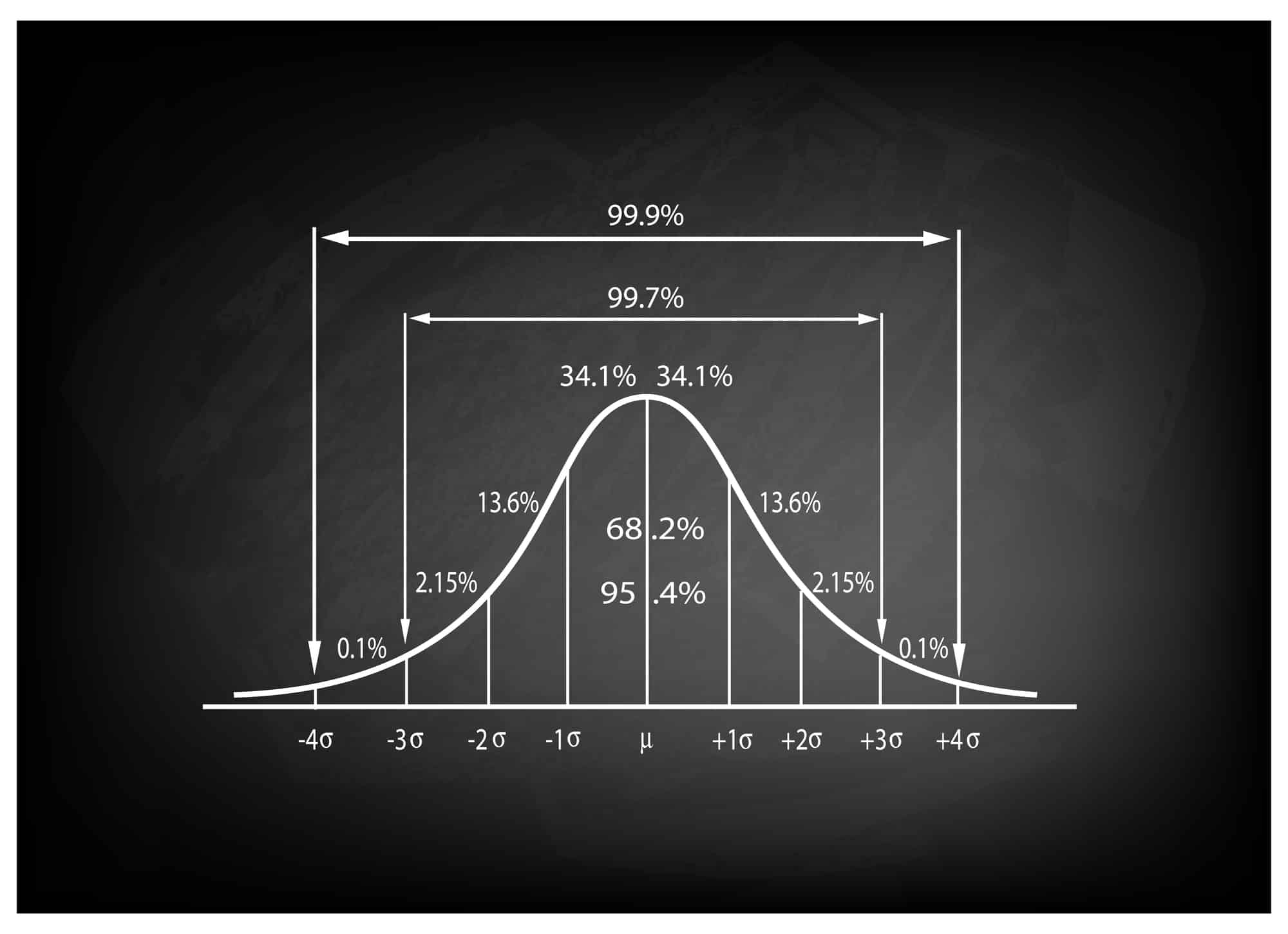
Para aprender a interpretar a tabela de pontuação z, primeiro você precisa saber a pontuação z para o valor que deseja pesquisar. A tabela de pontuação z normalmente mostra a área sob a curva normal padrão para um determinado intervalo de pontuações z.

Por exemplo, digamos que você queira encontrar a área sob a curva para um escore z de 1,5. Você procuraria na tabela de pontuação z a linha que corresponde à pontuação z de 1,5 e, em seguida, localizaria a coluna que corresponde à área sob a curva. O valor nessa célula é a área sob a curva para um escore z de 1,5.

A área sob a curva é a probabilidade de um determinado valor ocorrer. Por exemplo, se a área sob a curva para um escore z de 1,5 for 0,9332, haverá uma probabilidade de 93,32% de ocorrer um valor com um escore z de 1,5.

É importante observar que as tabelas de pontuação z geralmente se baseiam na curva normal padrão, que é uma distribuição normal com média 0 e desvio padrão 1. Se sua pontuação z for baseada em média e desvio padrão diferentes, você precisará usar uma fórmula de conversão de pontuação z para convertê-la na distribuição normal padrão antes de procurá-la na tabela.

Leia também: Como alterar nome de usuário e nome no Clubhouse Android

O que significa um escore Z negativo?

Um escore z negativo significa que o valor é menor que a média. Ou seja, está abaixo da média.

Para melhor compreensão, vamos pegar o exemplo anterior e dizer que você tem uma amostra de 1.000 pessoas e deseja encontrar o escore z para uma pessoa com 1,50 m de altura. A altura média da amostra é de 5 pés e 10 polegadas e o desvio padrão é de 2 polegadas. Para calcular o z-score para uma pessoa com 5 pés e 8 polegadas de altura, você usaria a seguinte fórmula:

z = (68 – 70) / 2 = -1

Isso significaria que a pessoa com 5 pés e 8 polegadas de altura está um desvio padrão abaixo da média.

Em geral, um escore z de 0 significa que um valor está exatamente na média, um escore z de 1 significa que um valor está um desvio padrão acima da média e um escore z de -1 significa que um valor está um desvio padrão abaixo da média.

Perguntas Frequentes (FAQ)

Q1. Como o Z-Score é usado na vida real?

Resp. O Z-score, também conhecido como pontuação padrão, é uma métrica para determinar quantos desvios padrão um número está da média do conjunto de dados. Encontrar outliers, anomalias e padrões estranhos em dados é uma tarefa típica em estatística, análise de dados e aprendizado de máquina.

Q2. O que produziria um escore z negativo?

Resp. Um escore Z negativo indica que um valor está abaixo da média do conjunto de dados. Em geral, qualquer valor menor que a média do conjunto de dados produzirá um escore Z negativo.

Q3. O que a tabela Z diz a você?

Resp. A tabela Z, também conhecida como tabela normal padrão, é uma tabela estatística que mostra a probabilidade de um determinado valor ocorrer dentro de uma distribuição normal padrão.

Recomendado:

• Como assistir a vídeos excluídos do YouTube
• Um guia completo para o princípio Modbus Slave
• Como INDEXAR Múltiplos Critérios no Planilhas Google
• Como funciona o GNSS?

Para interpretar um Z-score, é importante considerar a média e o desvio padrão do conjunto de dados, bem como o contexto em que o Z-score está sendo usado. Esperamos sinceramente poder fornecer algumas informações sobre como interpretar o escore z . Por favor, deixe-nos saber suas dúvidas e sugestões na seção de comentários abaixo.