Comment interpréter le score Z

Un score z est une mesure numérique qui décrit le nombre d'écarts types d'une valeur particulière par rapport à la moyenne d'un ensemble de données. Il est utilisé pour déterminer la rareté ou la fréquence d'une valeur particulière dans un ensemble de données. Mais comment trouver le score z? Continuez à lire l'article pour le savoir. Un score z peut être positif ou négatif, où un score z positif indique que la valeur est supérieure à la moyenne et un score z négatif indique que la valeur est inférieure à la moyenne. Nous verrons comment interpréter le score z plus loin dans l'article.

Comment interpréter le score Z

Dans cet article, vous connaîtrez les étapes pour interpréter le score Z en détail.

Qu'est-ce que le score Z ?

Un score z est une mesure qui quantifie le nombre d'écarts-types qu'une valeur donnée s'écarte de la moyenne de l'ensemble de données. Il est utilisé pour établir la rareté ou la prévalence d'une valeur spécifique dans un ensemble de données. Continuez à lire pour savoir comment interpréter le score z

Voyons les manières possibles d'apprendre à interpréter le score z :

1. Les scores Z sont mesurés en unités d'écart type

Lors de l'interprétation d'un score z, il est important de garder à l'esprit que les scores z sont mesurés en unités d'écart type. Cela signifie que la valeur du score z vous indique le nombre d'écarts types entre une valeur particulière et la moyenne de l'ensemble de données.

Par exemple, supposons que vous ayez un ensemble de données avec une moyenne de 50 et un écart type de 10. Si vous calculez le score z pour une valeur particulière, disons 30, et que vous trouvez qu'il est de -2, vous pouvez interpréter cela comme signifiant que la valeur de 30 est deux écarts-types en dessous de la moyenne de 50.

Vous pouvez également utiliser une table z pour déterminer le pourcentage de valeurs dans l'ensemble de données qui sont au-dessus ou en dessous d'un score z particulier. Par exemple, si vous avez un score z de 1,96, vous pouvez rechercher cette valeur dans un tableau z pour constater qu'environ 97,5 % des valeurs du jeu de données sont inférieures à cette valeur.

2. Les scores Z peuvent être positifs ou négatifs

Le fait que les scores z puissent être positifs ou négatifs est important lors de l'interprétation d'un score z, car il vous permet de déterminer si une valeur particulière est supérieure ou inférieure à la moyenne de l'ensemble de données et à quel point cette valeur est rare ou courante dans l'ensemble de données. Plus loin dans l'article, nous verrons ce que signifie un score z négatif

3. Les scores Z facilitent la comparaison de vos données avec d'autres mesures

Les scores z vous permettent de comparer facilement vos données à d'autres mesures, ce qui est important lors de l'interprétation d'un score z, car cela vous permet de mettre vos données en contexte et de prendre des décisions plus éclairées en fonction de votre analyse.

A lire également : Supprimer le mot de passe du fichier Excel

Comment trouver le score Z

Pour trouver le score z pour une valeur donnée, vous devez connaître la moyenne et l'écart type de la population ou de l'échantillon d'où provient la valeur. La formule de calcul du z-score est la suivante :

z = (x - moyenne) / écart type

Où x est la valeur, la moyenne est la moyenne de la population ou de l'échantillon et l'écart type est l'écart type de la population ou de l'échantillon.

Par exemple, supposons que vous ayez un échantillon de 1000 personnes et que vous souhaitiez trouver le score z pour une personne mesurant 1,80 mètre. La hauteur moyenne de l'échantillon est de 5 pieds 10 pouces et l'écart type est de 2 pouces. Pour calculer le score z pour une personne mesurant 6 pieds, vous utiliseriez la formule suivante :

z = (72 – 70) / 2 = 1

Cela signifierait que la personne qui mesure 6 pieds est à un écart type au-dessus de la moyenne.

Si vous souhaitez trouver le score z pour une valeur inférieure à la moyenne, le score z sera négatif. Par exemple, si la valeur est de 5 pieds 8 pouces, le score z serait :

z = (68 – 70) / 2 = -1

Cela signifierait que la personne qui mesure 5 pieds 8 pouces est un écart type en dessous de la moyenne.

Score Z vs écart type

Vous trouverez ci-dessous certaines des différences entre le score z et l'écart type.

Score Z	Écart-type
Le nombre d'écarts types entre un point de données et la moyenne	Une mesure de la propagation ou de la dispersion d'un ensemble de points de données autour de la moyenne
La formule pour le score z est (x - moyenne) / écart type	La formule de l'écart type est √((Σ(x – moyenne)^2) / n)
Vous indique le nombre d'écarts types entre un point de données et la moyenne	Vous indique à quel point les données sont réparties par rapport à la moyenne
Un score z de 1,5 signifie que le point de données est à 1,5 écart type au-dessus de la moyenne	Un écart type de 10 signifie que les points de données sont généralement à 10 unités de la moyenne

Ainsi, la principale différence entre le score z et l'écart type est qu'un score z est une mesure spécifique du nombre d'écarts types entre une valeur et la moyenne, tandis que la propagation des données est quantifiée par l'écart type.

A lire également : Basculer rapidement entre les feuilles de calcul

Comment interpréter le tableau des scores Z

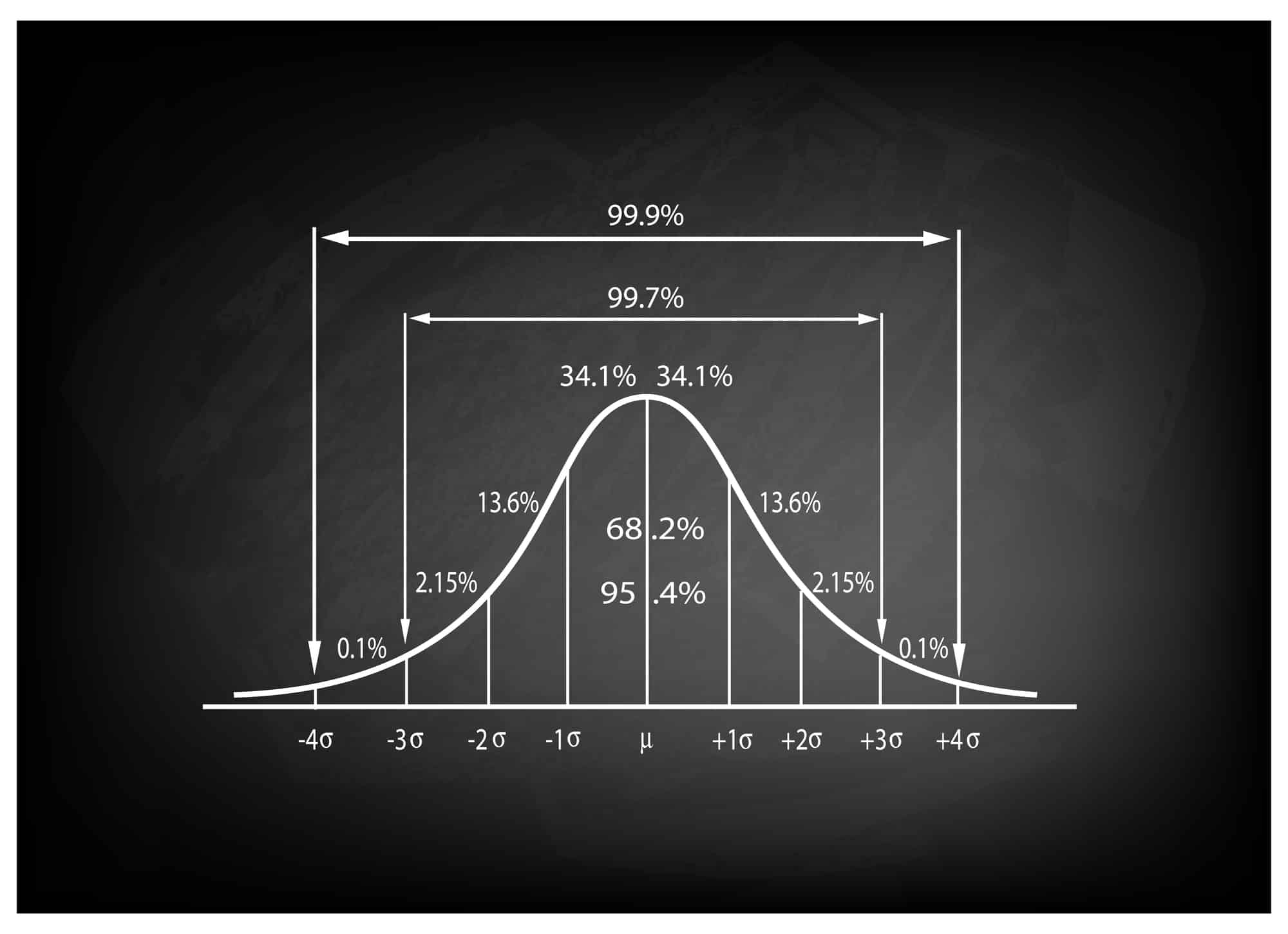
Afin d'apprendre à interpréter le tableau des scores z, vous devez d'abord connaître le score z pour la valeur que vous souhaitez rechercher. Le tableau des scores z vous montrera généralement la zone sous la courbe normale standard pour une plage donnée de scores z.

Par exemple, supposons que vous souhaitiez trouver l'aire sous la courbe pour un score z de 1,5. Vous recherchez dans le tableau des scores z la ligne qui correspond au score z de 1,5, puis recherchez la colonne qui correspond à l'aire sous la courbe. La valeur dans cette cellule est l'aire sous la courbe pour un score z de 1,5.

L'aire sous la courbe est la probabilité qu'une valeur donnée se produise. Par exemple, si l'aire sous la courbe pour un score z de 1,5 est de 0,9332, il y a une probabilité de 93,32 % qu'une valeur avec un score z de 1,5 se produise.

Il est important de noter que les tableaux de score z sont généralement basés sur la courbe normale standard, qui est une distribution normale avec une moyenne de 0 et un écart type de 1. Si votre score z est basé sur une moyenne et un écart type différents, vous devrez utiliser une formule de conversion du score z pour le convertir en distribution normale standard avant de le rechercher dans le tableau.

Lisez également: Comment changer le nom d'utilisateur et le nom sur Clubhouse Android

Que signifie un score Z négatif ?

Un score z négatif signifie que la valeur est inférieure à la moyenne. En d'autres termes, il est inférieur à la moyenne.

Pour une meilleure compréhension, prenons l'exemple précédent et disons que vous avez un échantillon de 1000 personnes et que vous voulez trouver le score z pour une personne qui mesure 5 pieds 8 pouces. La hauteur moyenne de l'échantillon est de 5 pieds 10 pouces et l'écart type est de 2 pouces. Pour calculer le score z d'une personne mesurant 5 pieds 8 pouces, vous utiliserez la formule suivante :

z = (68 – 70) / 2 = -1

Cela signifierait que la personne qui mesure 5 pieds 8 pouces est un écart type en dessous de la moyenne.

En général, un score z de 0 signifie qu'une valeur est exactement à la moyenne, un score z de 1 signifie qu'une valeur est à un écart type au-dessus de la moyenne et un score z de -1 signifie qu'une valeur est un écart type en dessous de la moyenne.

Foire aux questions (FAQ)

Q1. Comment le Z-Score est-il utilisé dans la vraie vie ?

Rép. Le score Z, également appelé score standard, est une mesure permettant de déterminer le nombre d'écarts types entre un nombre et la moyenne de l'ensemble de données. La recherche de valeurs aberrantes, d'anomalies et de modèles étranges dans les données est une tâche typique en statistique, en analyse de données et en apprentissage automatique.

Q2. Qu'est-ce qui produirait un score z négatif ?

Rép. Un score Z négatif indique qu'une valeur est inférieure à la moyenne de l'ensemble de données. En général, toute valeur inférieure à la moyenne de l'ensemble de données produira un score Z négatif.

Q3. Que vous dit la table Z ?

Rép. Le tableau Z, également connu sous le nom de tableau normal standard, est un tableau statistique qui montre la probabilité qu'une valeur donnée se produise dans une distribution normale standard.

Recommandé:

• Comment regarder des vidéos YouTube supprimées
• Un guide complet sur le principe de l'esclave Modbus
• Comment INDEXER MATCH plusieurs critères dans Google Sheets
• Comment fonctionne le GNSS ?

Pour interpréter un score Z, il est important de prendre en compte la moyenne et l'écart type de l'ensemble de données, ainsi que le contexte dans lequel le score Z est utilisé. Nous espérons sincèrement que nous pourrons fournir des informations sur la façon d'interpréter le score z . Veuillez nous faire part de vos questions et suggestions dans la section commentaires ci-dessous.