Cómo interpretar la puntuación Z

Una puntuación z es una medida numérica que describe el número de desviaciones estándar de un valor particular de la media de un conjunto de datos. Se utiliza para determinar qué tan raro o común es un valor particular en un conjunto de datos. Pero, ¿cómo encontrar la puntuación z? Sigue leyendo el artículo para averiguarlo. Una puntuación z puede ser positiva o negativa, donde una puntuación z positiva indica que el valor está por encima de la media y una puntuación z negativa indica que el valor está por debajo de la media. Discutiremos cómo interpretar la puntuación z más adelante en el artículo.

Cómo interpretar la puntuación Z

En este artículo, conocerá los pasos para interpretar el puntaje Z en detalle.

¿Qué es la puntuación Z?

Una puntuación z es una métrica que cuantifica cuántas desviaciones estándar se desvía un valor dado de la media del conjunto de datos. Se emplea para establecer la rareza o prevalencia de un valor específico dentro de un conjunto de datos. Siga leyendo para descubrir cómo interpretar la puntuación z

Veamos las posibles formas de aprender a interpretar el puntaje z:

1. Las puntuaciones Z se miden en unidades de desviación estándar

Al interpretar una puntuación z, es importante tener en cuenta que las puntuaciones z se miden en unidades de desviación estándar. Esto significa que el valor de la puntuación z le dice cuántas desviaciones estándar hay un valor particular de la media del conjunto de datos.

Por ejemplo, suponga que tiene un conjunto de datos con una media de 50 y una desviación estándar de 10. Si calcula la puntuación z para un valor particular, digamos 30, y encuentra que es -2, puede interpretar esto como que el valor de 30 está dos desviaciones estándar por debajo de la media de 50.

También puede usar una tabla z para determinar el porcentaje de valores en el conjunto de datos que están por encima o por debajo de una puntuación z particular. Por ejemplo, si tiene una puntuación z de 1,96, puede buscar este valor en una tabla z para encontrar que aproximadamente el 97,5 % de los valores en el conjunto de datos están por debajo de este valor.

2. Los puntajes Z pueden ser positivos o negativos

El hecho de que las puntuaciones z puedan ser positivas o negativas es importante al interpretar una puntuación z porque le permite determinar si un valor particular está por encima o por debajo de la media del conjunto de datos y qué tan raro o común es ese valor en el conjunto de datos. Más adelante en el artículo verá qué significa un puntaje z negativo

3. Los puntajes Z simplifican la comparación de sus datos con otras métricas

Los puntajes z le permiten comparar sus datos fácilmente con otras métricas, lo cual es importante al interpretar un puntaje z porque le permite poner sus datos en contexto y tomar decisiones más informadas basadas en su análisis.

Lea también: Quitar la contraseña del archivo de Excel

Cómo encontrar la puntuación Z

Para encontrar el puntaje z para un valor dado, necesitará conocer la media y la desviación estándar de la población o muestra de donde proviene el valor. La fórmula de cálculo de la puntuación z es la siguiente:

z = (x – media) / desviación estándar

Donde x es el valor, la media es la media de la población o muestra y la desviación estándar es la desviación estándar de la población o muestra.

Por ejemplo, supongamos que tiene una muestra de 1000 personas y desea encontrar el puntaje z para una persona que mide 6 pies de altura. La altura media de la muestra es de 5 pies, 10 pulgadas y la desviación estándar es de 2 pulgadas. Para calcular el puntaje z para una persona que mide 6 pies de altura, usaría la siguiente fórmula:

z = (72 – 70) / 2 = 1

Esto significaría que la persona que mide 6 pies de altura está una desviación estándar por encima de la media.

Si desea encontrar el puntaje z para un valor que está por debajo de la media, el puntaje z será negativo. Por ejemplo, si el valor es 5 pies, 8 pulgadas, la puntuación z sería:

z = (68 – 70) / 2 = -1

Esto significaría que la persona que mide 5 pies y 8 pulgadas está una desviación estándar por debajo de la media.

Puntuación Z frente a desviación estándar

A continuación se enumeran algunas de las diferencias entre la puntuación z y la desviación estándar.

puntuación Z	Desviación Estándar
El número de desviaciones estándar de un punto de datos con respecto a la media	Una medida de la propagación o dispersión de un conjunto de puntos de datos alrededor de la media
La fórmula para la puntuación z es (x – media) / desviación estándar	La fórmula para la desviación estándar es √((Σ(x – media)^2) / n)
Le dice cuántas desviaciones estándar es un punto de datos de la media	Le dice qué tan separados están los datos de la media
Una puntuación z de 1,5 significa que el punto de datos está 1,5 desviaciones estándar por encima de la media	Una desviación estándar de 10 significa que los puntos de datos suelen estar a 10 unidades de la media

Entonces, la principal diferencia entre el puntaje z y la desviación estándar es que un puntaje z es una medida específica de cuántas desviaciones estándar hay un valor de la media, mientras que la dispersión de datos se cuantifica por la desviación estándar.

Lea también: Cambiar rápidamente entre hojas de trabajo

Cómo interpretar la tabla de puntuación Z

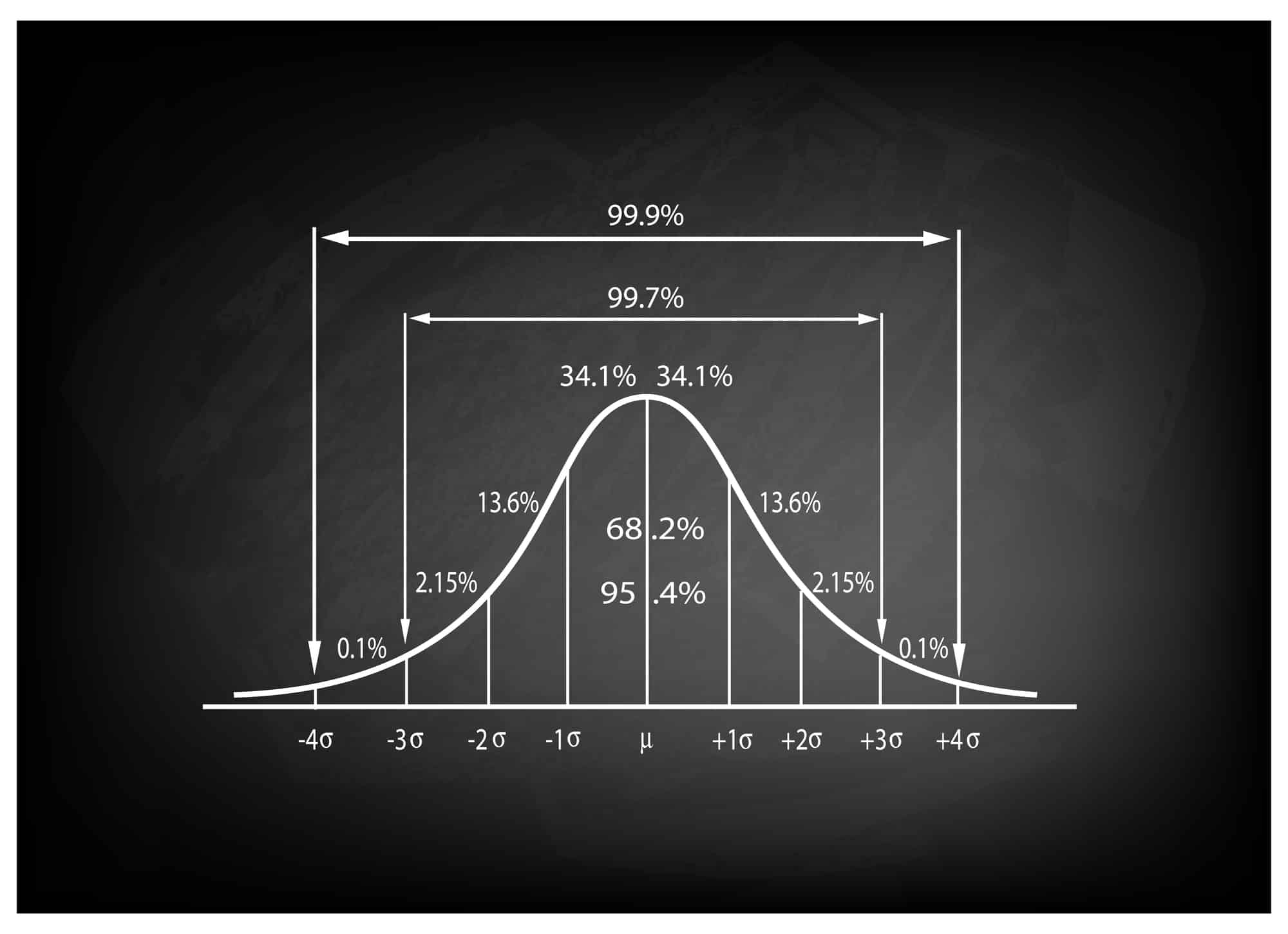
Para aprender a interpretar la tabla de puntuación z, primero debe conocer la puntuación z del valor que desea buscar. La tabla de puntajes z generalmente le mostrará el área bajo la curva normal estándar para un rango determinado de puntajes z.

Por ejemplo, supongamos que desea encontrar el área bajo la curva para una puntuación z de 1,5. Buscaría en la tabla de puntuación z la fila que corresponde a la puntuación z de 1,5 y luego encontraría la columna que corresponde al área bajo la curva. El valor en esa celda es el área bajo la curva para una puntuación z de 1,5.

El área bajo la curva es la probabilidad de que ocurra un valor dado. Por ejemplo, si el área bajo la curva para una puntuación z de 1,5 es 0,9332, entonces hay una probabilidad del 93,32 % de que se produzca un valor con una puntuación z de 1,5.

Es importante tener en cuenta que las tablas de puntuación z generalmente se basan en la curva normal estándar, que es una distribución normal con una media de 0 y una desviación estándar de 1. Si su puntuación z se basa en una media y una desviación estándar diferentes, necesitará usar una fórmula de conversión de puntuación z para convertirla a la distribución normal estándar antes de buscarla en la tabla.

Lea también: Cómo cambiar el nombre de usuario y el nombre en Clubhouse Android

¿Qué significa un puntaje Z negativo?

Una puntuación z negativa significa que el valor es menor que la media. En otras palabras, está por debajo de la media.

Para una mejor comprensión, tomemos el ejemplo anterior y digamos que tiene una muestra de 1000 personas y desea encontrar el puntaje z para una persona que mide 5 pies y 8 pulgadas de alto. La altura media de la muestra es de 5 pies, 10 pulgadas y la desviación estándar es de 2 pulgadas. Para calcular el puntaje z para una persona que mide 5 pies y 8 pulgadas de alto, usaría la siguiente fórmula:

z = (68 – 70) / 2 = -1

Esto significaría que la persona que mide 5 pies y 8 pulgadas de alto está una desviación estándar por debajo de la media.

En general, una puntuación z de 0 significa que un valor está exactamente en la media, una puntuación z de 1 significa que un valor está una desviación estándar por encima de la media y una puntuación z de -1 significa que un valor está una desviación estándar por debajo de la media.

Preguntas frecuentes (FAQ)

Q1. ¿Cómo se usa Z-Score en la vida real?

Respuesta La puntuación Z, también conocida como puntuación estándar, es una métrica para determinar cuántas desviaciones estándar tiene un número con respecto a la media del conjunto de datos. Encontrar valores atípicos, anomalías y patrones extraños en los datos es una tarea típica en estadística, análisis de datos y aprendizaje automático.

Q2. ¿Qué produciría una puntuación z negativa?

Respuesta Una puntuación Z negativa indica que un valor está por debajo de la media del conjunto de datos. En general, cualquier valor que sea menor que la media del conjunto de datos producirá una puntuación Z negativa.

Q3. ¿Qué te dice la tabla Z?

Respuesta La tabla Z, también conocida como tabla normal estándar, es una tabla estadística que muestra la probabilidad de que un valor dado ocurra dentro de una distribución normal estándar.

Recomendado:

• Cómo ver videos eliminados de YouTube
• Una guía completa sobre el principio de Modbus Slave
• Cómo INDEX COINCIDIR con múltiples criterios en Hojas de cálculo de Google
• ¿Cómo funciona el GNSS?

Para interpretar una puntuación Z, es importante tener en cuenta la media y la desviación estándar del conjunto de datos, así como el contexto en el que se utiliza la puntuación Z. Esperamos sinceramente poder proporcionar alguna información sobre cómo interpretar la puntuación z . Háganos saber sus consultas y sugerencias en la sección de comentarios a continuación.