So interpretieren Sie den Z-Score

Ein Z-Score ist ein numerisches Maß, das die Anzahl der Standardabweichungen eines bestimmten Werts vom Mittelwert eines Datensatzes beschreibt. Es wird verwendet, um zu bestimmen, wie selten oder häufig ein bestimmter Wert in einem Datensatz vorkommt. Aber wie findet man den Z-Score? Lesen Sie den Artikel weiter, um es herauszufinden. Ein Z-Score kann positiv oder negativ sein, wobei ein positiver Z-Score angibt, dass der Wert über dem Mittelwert liegt, und ein negativer Z-Score angibt, dass der Wert unter dem Mittelwert liegt. Wir werden in diesem Artikel weiter besprechen, wie der Z-Score zu interpretieren ist.

So interpretieren Sie den Z-Score

In diesem Artikel erfahren Sie mehr über die Schritte zur Interpretation des Z-Scores im Detail.

Was ist der Z-Score?

Ein Z-Score ist eine Metrik, die quantifiziert, wie viele Standardabweichungen ein bestimmter Wert vom Mittelwert des Datensatzes abweicht. Es wird verwendet, um die Seltenheit oder Prävalenz eines bestimmten Werts innerhalb eines Datensatzes festzustellen. Lesen Sie weiter, um herauszufinden, wie man den Z-Score interpretiert

Sehen wir uns die Möglichkeiten an, um zu lernen, wie man den Z-Score interpretiert:

1. Z-Scores werden in Standardabweichungseinheiten gemessen

Bei der Interpretation eines Z-Scores ist zu beachten, dass Z-Scores in Standardabweichungseinheiten gemessen werden. Das bedeutet, dass der Wert des Z-Scores angibt, wie viele Standardabweichungen ein bestimmter Wert vom Mittelwert des Datensatzes entfernt ist.

Angenommen, Sie haben einen Datensatz mit einem Mittelwert von 50 und einer Standardabweichung von 10. Wenn Sie den Z-Wert für einen bestimmten Wert berechnen, sagen wir 30, und feststellen, dass er -2 ist, können Sie dies so interpretieren, dass dies der Fall ist der Wert von 30 liegt zwei Standardabweichungen unter dem Mittelwert von 50.

Sie können auch eine Z-Tabelle verwenden, um den Prozentsatz der Werte im Dataset zu bestimmen, die über oder unter einem bestimmten Z-Score liegen. Wenn Sie beispielsweise einen Z-Wert von 1,96 haben, können Sie diesen Wert in einer Z-Tabelle nachschlagen und feststellen, dass etwa 97,5 % der Werte im Dataset unter diesem Wert liegen.

2. Z-Scores können positiv oder negativ sein

Die Tatsache, dass Z-Scores positiv oder negativ sein können, ist bei der Interpretation eines Z-Scores wichtig, da Sie damit feststellen können, ob ein bestimmter Wert über oder unter dem Mittelwert des Datensatzes liegt und wie selten oder häufig dieser Wert im Datensatz vorkommt. Weiter unten in diesem Artikel erfahren Sie, was ein negativer Z-Score bedeutet

3. Z-Scores machen es einfach, Ihre Daten mit anderen Metriken zu vergleichen

Mit Z-Scores können Sie Ihre Daten einfach mit anderen Metriken vergleichen, was bei der Interpretation eines Z-Scores wichtig ist, da Sie Ihre Daten in einen Kontext stellen und basierend auf Ihrer Analyse fundiertere Entscheidungen treffen können.

Lesen Sie auch: Passwort aus Excel-Datei entfernen

So finden Sie den Z-Score

Um den Z-Score für einen bestimmten Wert zu finden, müssen Sie den Mittelwert und die Standardabweichung der Grundgesamtheit oder Stichprobe kennen, aus der der Wert stammt. Die Berechnungsformel für den Z-Score lautet wie folgt:

z = (x – Mittelwert) / Standardabweichung

Dabei ist x der Wert, Mittelwert der Mittelwert der Grundgesamtheit oder Stichprobe und Standardabweichung die Standardabweichung der Grundgesamtheit oder Stichprobe.

Angenommen, Sie haben eine Stichprobe von 1000 Personen und möchten den z-Wert für eine 1,80 m große Person ermitteln. Die mittlere Höhe der Probe beträgt 5 Fuß, 10 Zoll und die Standardabweichung beträgt 2 Zoll. Um den z-Wert für eine 1,80 m große Person zu berechnen, würden Sie die folgende Formel verwenden:

z = (72 – 70) / 2 = 1

Dies würde bedeuten, dass die Person, die 6 Fuß groß ist, eine Standardabweichung über dem Mittelwert liegt.

Wenn Sie den Z-Score für einen Wert finden möchten, der unter dem Mittelwert liegt, ist der Z-Score negativ. Wenn der Wert beispielsweise 5 Fuß, 8 Zoll beträgt, lautet der Z-Wert:

z = (68 – 70) / 2 = -1

Dies würde bedeuten, dass die Person, die 5 Fuß, 8 Zoll groß ist, eine Standardabweichung unter dem Mittelwert liegt.

Z-Score vs. Standardabweichung

Unten aufgeführt sind einige der Unterschiede zwischen dem Z-Score und der Standardabweichung.

Z-Punktzahl	Standardabweichung
Die Anzahl der Standardabweichungen, die ein Datenpunkt vom Mittelwert hat	Ein Maß für die Streuung oder Streuung einer Reihe von Datenpunkten um den Mittelwert
Die Formel für den Z-Score lautet (x – Mittelwert) / Standardabweichung	Die Formel für die Standardabweichung lautet √((Σ(x – Mittelwert)^2) / n)
Gibt an, wie viele Standardabweichungen ein Datenpunkt vom Mittelwert entfernt ist	Gibt an, wie weit die Daten vom Mittelwert entfernt sind
Ein Z-Score von 1,5 bedeutet, dass der Datenpunkt 1,5 Standardabweichungen über dem Mittelwert liegt	Eine Standardabweichung von 10 bedeutet, dass die Datenpunkte typischerweise 10 Einheiten vom Mittelwert entfernt sind

Der Hauptunterschied zwischen Z-Score und Standardabweichung besteht also darin, dass ein Z-Score ein spezifisches Maß dafür ist, wie viele Standardabweichungen ein Wert vom Mittelwert entfernt ist, während die Datenstreuung durch die Standardabweichung quantifiziert wird.

Lesen Sie auch: Schnell zwischen Arbeitsblättern wechseln

So interpretieren Sie die Z-Score-Tabelle

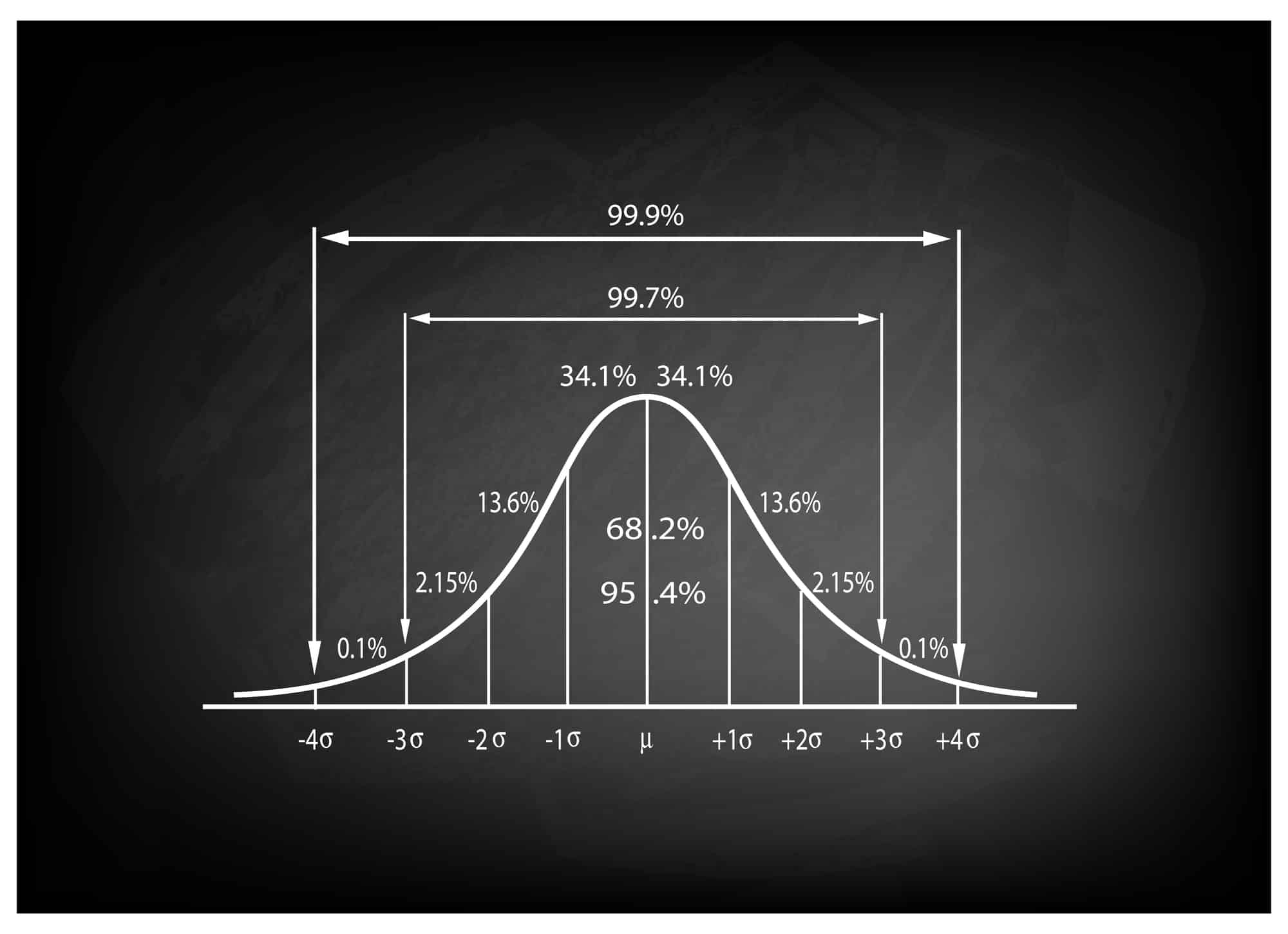
Um zu lernen, wie man die Z-Score-Tabelle interpretiert, müssen Sie zuerst den Z-Score für den Wert kennen, den Sie nachschlagen möchten. Die Z-Score-Tabelle zeigt Ihnen normalerweise die Fläche unter der Standard-Normalkurve für einen bestimmten Bereich von Z-Scores.

Angenommen, Sie möchten die Fläche unter der Kurve für einen Z-Wert von 1,5 ermitteln. Sie würden in der Z-Score-Tabelle nach der Zeile suchen, die dem Z-Score von 1,5 entspricht, und dann die Spalte finden, die der Fläche unter der Kurve entspricht. Der Wert in dieser Zelle ist die Fläche unter der Kurve für einen Z-Score von 1,5.

Die Fläche unter der Kurve ist die Wahrscheinlichkeit, dass ein gegebener Wert auftritt. Wenn beispielsweise die Fläche unter der Kurve für einen Z-Score von 1,5 0,9332 beträgt, dann liegt eine Wahrscheinlichkeit von 93,32 % vor, dass ein Wert mit einem Z-Score von 1,5 auftritt.

Es ist wichtig zu beachten, dass Z-Score-Tabellen normalerweise auf der Standardnormalkurve basieren, bei der es sich um eine Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1 handelt. Wenn Ihr Z-Score auf einem anderen Mittelwert und einer anderen Standardabweichung basiert, Sie müssen eine Umrechnungsformel für den Z-Wert verwenden, um ihn in die Standardnormalverteilung umzuwandeln, bevor Sie ihn in der Tabelle nachschlagen.

Lesen Sie auch: So ändern Sie Benutzernamen und Namen auf Clubhouse Android

Was bedeutet ein negativer Z-Score?

Ein negativer Z-Score bedeutet, dass der Wert unter dem Mittelwert liegt. Mit anderen Worten, es liegt unter dem Mittelwert.

Nehmen wir zum besseren Verständnis das vorherige Beispiel und nehmen an, Sie haben eine Stichprobe von 1000 Personen und möchten den Z-Wert für eine Person ermitteln, die 5 Fuß, 8 Zoll groß ist. Die mittlere Höhe der Probe beträgt 5 Fuß, 10 Zoll, und die Standardabweichung beträgt 2 Zoll. Um den z-Wert für eine Person zu berechnen, die 5 Fuß, 8 Zoll groß ist, würden Sie die folgende Formel verwenden:

z = (68 – 70) / 2 = -1

Dies würde bedeuten, dass die Person, die 5 Fuß, 8 Zoll groß ist, eine Standardabweichung unter dem Mittelwert liegt.

Im Allgemeinen bedeutet ein Z-Score von 0, dass ein Wert genau auf dem Mittelwert liegt, ein Z-Score von 1, dass ein Wert eine Standardabweichung über dem Mittelwert liegt, und ein Z-Score von -1, dass ein Wert genau auf dem Mittelwert liegt eine Standardabweichung unter dem Mittelwert.

Häufig gestellte Fragen (FAQs)

Q1. Wie wird der Z-Score im wirklichen Leben verwendet?

Ans. Der Z-Wert, auch als Standardwert bezeichnet, ist eine Metrik zur Bestimmung, wie viele Standardabweichungen eine Zahl vom Mittelwert des Datensatzes entfernt ist. Das Auffinden von Ausreißern, Anomalien und seltsamen Mustern in Daten ist eine typische Aufgabe in Statistik, Datenanalyse und maschinellem Lernen.

Q2. Was würde zu einem negativen Z-Score führen?

Ans. Ein negativer Z-Score zeigt an, dass ein Wert unter dem Mittelwert des Datensatzes liegt. Im Allgemeinen führt jeder Wert, der kleiner als der Mittelwert des Datensatzes ist, zu einem negativen Z-Score.

Q3. Was sagt Ihnen die Z-Tabelle?

Ans. Die Z-Tabelle, auch Standard-Normaltabelle genannt, ist eine statistische Tabelle, die die Wahrscheinlichkeit zeigt, dass ein bestimmter Wert innerhalb einer Standard-Normalverteilung auftritt.

Empfohlen:

• So sehen Sie sich gelöschte YouTube-Videos an
• Eine vollständige Anleitung zum Modbus-Slave-Prinzip
• So INDEXIEREN Sie mehrere Kriterien in Google Sheets
• Wie funktioniert GNSS?

Um einen Z-Score zu interpretieren, ist es wichtig, den Mittelwert und die Standardabweichung des Datensatzes sowie den Kontext zu berücksichtigen, in dem der Z-Score verwendet wird. Wir hoffen aufrichtig, dass wir Ihnen einige Informationen zur Interpretation von z score geben konnten. Bitte teilen Sie uns Ihre Fragen und Vorschläge im Kommentarbereich unten mit.